Problema celor două corpuri [ ] Ne propunem determinarea ecuaţiilor de mişcare pentru două corpuri de mase
m
1
{\displaystyle m_1 \!}
m
2
{\displaystyle m_2 \!}
F
→
=
f
(
r
)
⋅
r
^
=
−
∂
U
∂
r
⋅
r
^
;
{\displaystyle {\vec {F}}=f(r)\cdot {\hat {r}}=-{\frac {\partial U}{\partial r}}\cdot {\hat {r}};\!}
(1)
r
^
=
r
→
r
=
r
1
−
r
2
|
r
1
−
r
2
|
;
{\displaystyle {\hat {r}}={\frac {\vec {r}}{r}}={\frac {r_{1}-r_{2}}{|r_{1}-r_{2}|}};\!}
(2)
r
→
=
r
→
1
−
r
→
2
.
{\displaystyle {\vec {r}}={\vec {r}}_{1}-{\vec {r}}_{2}.\!}
(3) Poziţia centrului de masă (CM ):
R
→
=
m
1
r
→
1
+
m
2
r
→
2
m
1
+
m
2
{\displaystyle {\vec {R}}={\frac {m_{1}{\vec {r}}_{1}+m_{2}{\vec {r}}_{2}}{m_{1}+m_{2}}}\!}
(4)
Exprimăm vectorii
r
1
{\displaystyle r_1 \!}
r
2
{\displaystyle r_2 \!}
r
→
{\displaystyle \vec r \!}
R
→
:
{\displaystyle {\vec {R}}:\!}
r
→
=
r
→
1
−
r
→
2
(
m
1
+
m
2
)
⋅
R
→
m
2
=
m
1
m
2
r
→
1
+
r
2
}
⇒
r
→
1
=
m
2
m
1
+
m
2
(
r
→
+
(
m
1
+
m
2
)
R
→
m
2
)
{\displaystyle \left.{\begin{matrix}{\vec {r}}={\vec {r}}_{1}-{\vec {r}}_{2}\\{\frac {(m_{1}+m_{2})\cdot {\vec {R}}}{m_{2}}}={\frac {m_{1}}{m_{2}}}{\vec {r}}_{1}+r_{2}\end{matrix}}\right\}\;\Rightarrow \;{\vec {r}}_{1}={\frac {m_{2}}{m_{1}+m_{2}}}\left({\vec {r}}+{\frac {(m_{1}+m_{2}){\vec {R}}}{m_{2}}}\right)\!}
(5)
μ
p
o
z
i
t
r
o
n
=
m
e
⋅
m
e
(
m
e
+
m
e
)
=
m
e
2
{\displaystyle \mu _{pozitron}={\frac {m_{e}\cdot m_{e}}{(m_{e}+m_{e})}}={\frac {m_{e}}{2}}\!}
m
(
p
)
≫
m
(
e
+
)
{\displaystyle m(p)\gg m(e^{+})\!}
μ
h
i
d
r
o
g
e
n
=
m
p
m
e
(
m
p
+
m
e
)
≈
m
e
{\displaystyle \mu _{hidrogen}={\frac {m_{p}m_{e}}{(m_{p}+m_{e})}}\approx m_{e}\!}
r
→
1
=
R
→
+
m
2
m
1
+
m
2
r
→
{\displaystyle {\vec {r}}_{1}={\vec {R}}+{\frac {m_{2}}{m_{1}+m_{2}}}{\vec {r}}\!}
(6)
r
→
2
=
R
→
−
m
1
m
1
+
m
2
r
→
{\displaystyle {\vec {r}}_{2}={\vec {R}}-{\frac {m_{1}}{m_{1}+m_{2}}}{\vec {r}}\!}
(7) Lagrange pentru sistem devine:
L
=
1
2
m
1
r
˙
1
2
+
1
2
m
2
r
˙
2
2
−
U
(
r
)
=
{\displaystyle L={\frac {1}{2}}m_{1}{\dot {r}}_{1}^{2}+{\frac {1}{2}}m_{2}{\dot {r}}_{2}^{2}-U(r)=\!}
(8)
deci
L
=
m
1
2
(
R
→
˙
+
m
2
M
r
→
˙
)
2
+
m
2
2
(
R
→
˙
−
m
1
M
r
→
˙
)
2
−
U
(
r
)
{\displaystyle L={\frac {m_{1}}{2}}\left({\dot {\vec {R}}}+{\frac {m_{2}}{M}}{\dot {\vec {r}}}\right)^{2}+{\frac {m_{2}}{2}}\left({\dot {\vec {R}}}-{\frac {m_{1}}{M}}{\dot {\vec {r}}}\right)^{2}-U(r)\!}
(9)
unde
M
=
m
1
+
m
2
{\displaystyle M = m_1+m_2 \!}
notând:
μ
=
m
1
m
2
m
1
+
m
2
{\displaystyle \mu ={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}\!}
(10) (masa redusă a sistemului)
Rezultă:
L
=
1
2
M
R
˙
2
+
1
2
μ
r
˙
2
−
U
(
r
)
.
{\displaystyle L={\frac {1}{2}}M{\dot {R}}^{2}+{\frac {1}{2}}\mu {\dot {r}}^{2}-U(r).\!}
(11) Aceleaşi rezultate obţinem alegând CM ca noua origine a sistemului.
r
→
1
′
=
r
→
1
−
R
→
{\displaystyle {\vec {r}}'_{1}={\vec {r}}_{1}-{\vec {R}}\!}
(12)
r
→
2
′
=
r
→
2
−
R
→
{\displaystyle {\vec {r}}'_{2}={\vec {r}}_{2}-{\vec {R}}\!}
(13) Conform teoremei lui König :
m
1
r
→
1
′
+
m
2
r
→
2
′
=
0.
{\displaystyle m_{1}{\vec {r}}'_{1}+m_{2}{\vec {r}}'_{2}=0.\!}
(14) Notând:
M
=
m
1
+
m
2
r
→
=
r
→
1
−
r
→
2
=
r
→
1
′
−
r
→
2
′
.
{\displaystyle M=m_{1}+m_{2}\;\;{\vec {r}}={\vec {r}}_{1}-{\vec {r}}_{2}={\vec {r}}'_{1}-{\vec {r}}'_{2}.\!}
(15)
r
→
1
′
=
m
2
M
r
→
r
→
2
′
=
m
1
M
r
→
{\displaystyle {\vec {r}}'_{1}={\frac {m_{2}}{M}}{\vec {r}}\;\;{\vec {r}}'_{2}={\frac {m_{1}}{M}}{\vec {r}}\!}
(16)
L
=
1
2
M
V
C
M
2
+
1
2
μ
r
˙
2
−
U
(
r
)
{\displaystyle L={\frac {1}{2}}MV_{CM}^{2}+{\frac {1}{2}}\mu {\dot {r}}^{2}-U(r)\!}
(17)
1
2
M
R
˙
2
+
1
2
μ
r
˙
2
−
U
(
r
)
{\displaystyle {\frac {1}{2}}M{\dot {R}}^{2}+{\frac {1}{2}}\mu {\dot {r}}^{2}-U(r)\!}
(18) a)
∂
L
∂
R
˙
=
M
R
˙
∂
L
∂
R
=
0
}
⇒
d
d
t
(
∂
l
∂
R
˙
)
−
∂
L
∂
R
=
0
⇒
M
R
¨
=
0
⇒
M
R
˙
=
c
o
n
s
t
{\displaystyle \left.{\begin{matrix}{\frac {\partial L}{\partial {\dot {R}}}}=M{\dot {R}}\\\\{\frac {\partial L}{\partial R}}=0\end{matrix}}\right\}\;\Rightarrow \;{\frac {d}{dt}}\left({\frac {\partial l}{\partial {\dot {R}}}}\right)-{\frac {\partial L}{\partial R}}=0\;\Rightarrow \;M{\ddot {R}}=0\;\Rightarrow \;M{\dot {R}}=const\!}
(19)
M
R
˙
=
M
(
m
1
r
˙
1
+
m
2
r
˙
2
m
1
+
m
2
)
=
m
1
r
˙
1
+
m
2
r
˙
2
=
p
1
+
p
2
M
R
˙
=
p
T
o
t
a
l
}
⇒
p
T
o
t
a
l
=
p
1
+
p
2
{\displaystyle \left.{\begin{matrix}M{\dot {R}}=M\left({\frac {m_{1}{\dot {r}}_{1}+m_{2}{\dot {r}}_{2}}{m_{1}+m_{2}}}\right)=m_{1}{\dot {r}}_{1}+m_{2}{\dot {r}}_{2}=p_{1}+p_{2}\\\\M{\dot {R}}=p_{Total}\end{matrix}}\right\}\;\Rightarrow \;p_{Total}=p_{1}+p_{2}\!}
(20) Deci impulsul total se conservă.
b)
∂
L
∂
r
˙
=
μ
r
˙
∂
L
∂
r
=
−
∂
U
∂
r
r
r
=
−
∂
U
∂
r
r
^
}
⇒
d
d
t
(
∂
L
∂
r
˙
)
−
∂
L
∂
r
=
0
⇒
μ
r
¨
+
∂
U
∂
r
r
^
=
0
{\displaystyle \left.{\begin{matrix}{\frac {\partial L}{\partial {\dot {r}}}}=\mu {\dot {r}}\\\\{\frac {\partial L}{\partial r}}=-{\frac {\partial U}{\partial r}}{\frac {r}{r}}=-{\frac {\partial U}{\partial r}}{\hat {r}}\end{matrix}}\right\}\;\Rightarrow \;{\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {r}}}}\right)-{\frac {\partial L}{\partial r}}=0\;\Rightarrow \;\mu {\ddot {r}}+{\frac {\partial U}{\partial r}}{\hat {r}}=0\!}
(21)
Concluzii [ ] Mişcarea a două puncte materiale care interacţionează între ele se reduce la problema mişcării unui punct de masă
μ
{\displaystyle \mu \!}
Observăm că a) şi b) nu sunt cuplate şi deci mişcarea
C
M
R
(
t
)
{\displaystyle \mathbf {CM} R(t)\!}
r
(
t
)
.
{\displaystyle \mathbf {r} (t).\!}
Putem ignora mişcarea
C
M
R
(
t
)
.
{\displaystyle \mathbf {CM} R(t).\!}
Sistemul câmpului central de forţe are simetrie sferică.
⇒
{\displaystyle \Rightarrow \!}
Se poate roti în jurul oricărei axe care trece prin origine.
⇒
{\displaystyle \Rightarrow \!}
Simetrie rotaţională:
Lagragianul nu depinde de direcţie:
L
=
T
(
r
˙
2
)
−
U
(
r
)
{\displaystyle L=T({\dot {r}}^{2})-U(r)\!}
(22)
⇒
{\displaystyle \Rightarrow \!}
Momentul unghiular se conservă:
L
=
r
×
p
=
c
o
n
s
t
.
{\displaystyle L=r\times p=const.\!}
(23)
L
→
⋅
r
→
=
(
r
→
×
p
→
)
⋅
r
→
=
0
{\displaystyle {\vec {L}}\cdot {\vec {r}}=({\vec {r}}\times {\vec {p}})\cdot {\vec {r}}=0\!}
(24)
r
→
⊥
L
→
{\displaystyle {\vec {r}}\perp {\vec {L}}\!}
(25)
⇒
{\displaystyle \Rightarrow \!}
Traiectoria
r
→
(
t
)
{\displaystyle \vec r(t) \!}
L
→
.
{\displaystyle {\vec {L}}.\!}
⇒
{\displaystyle \Rightarrow \!}
Putem parametriza traiectoria
r
→
(
t
)
{\displaystyle \vec r(t) \!}
coordonate polare :
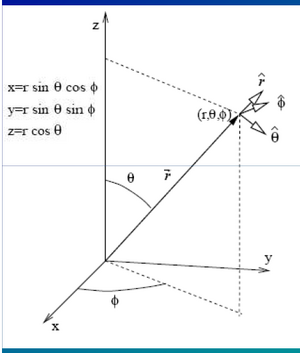
r
→
˙
=
r
e
^
+
r
φ
˙
e
^
θ
{\displaystyle {\dot {\vec {r}}}=r{\hat {e}}+r{\dot {\varphi }}{\hat {e}}_{\theta }\!}
(26) Lagrangianul în coordonate polare va fi:
L
=
1
2
μ
(
r
˙
2
+
r
2
φ
˙
2
)
−
U
(
r
)
{\displaystyle L={\frac {1}{2}}\mu ({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2})-U(r)\!}
(27) Observăm că
φ
{\displaystyle \varphi \!}
p
φ
{\displaystyle p_{\varphi }\!}
p
φ
=
∂
L
∂
φ
˙
=
μ
r
2
φ
˙
≡
l
{\displaystyle p_{\varphi }={\frac {\partial L}{\partial {\dot {\varphi }}}}=\mu r^{2}{\dot {\varphi }}\equiv l\!}
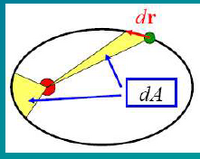
(28) (mărimea momentului unghiular)Introducem noţiunea de viteză areolară
Legea a II-a a lui Kepler :
Vectorul de poziţie al unei planete mătură arii egale în intervale de timp egale.
d
A
=
1
2
r
→
(
r
→
d
φ
)
=
1
2
r
2
d
φ
{\displaystyle {\mathit {d}}A={\frac {1}{2}}{\vec {r}}({\vec {r}}{\mathit {d}}\varphi )={\frac {1}{2}}r^{2}{\mathit {d}}\varphi \!}
(29) Rezultă viteza areolară:
d
A
d
t
=
1
2
r
2
φ
=
1
2
l
μ
=
c
o
n
s
t
.
{\displaystyle {\frac {{\mathit {d}}A}{{\mathit {d}}t}}={\frac {1}{2}}r^{2}\varphi ={\frac {1}{2}}{\frac {l}{\mu }}=const.\!}
(30) Mişcarea planetei este mai rapidă când orbita este mai apropiată de origine.
d
d
t
(
∂
L
∂
r
˙
)
−
∂
L
∂
r
˙
=
0
⇒
μ
r
¨
−
μ
r
φ
˙
2
+
∂
U
∂
r
=
0
{\displaystyle {\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {r}}}}\right)-{\frac {\partial L}{\partial {\dot {r}}}}=0\;\Rightarrow \;\mu {\ddot {r}}-\mu r{\dot {\varphi }}^{2}+{\frac {\partial U}{\partial r}}=0\!}
(31) unde
μ
r
φ
˙
2
{\displaystyle \mu r{\dot {\varphi }}^{2}\!}
(32) este forţa centrifugă, iar
∂
U
∂
r
{\displaystyle {\frac {\partial U}{\partial r}}\!}
(33) este forţa centrală.
φ
˙
=
l
μ
r
2
{\displaystyle {\dot {\varphi }}={\frac {l}{\mu r^{2}}}\!}
(33)
deci
μ
r
¨
−
l
2
μ
r
3
+
∂
U
∂
r
=
0
{\displaystyle \mu {\ddot {r}}-{\frac {l^{2}}{\mu r^{3}}}+{\frac {\partial U}{\partial r}}=0\!}
(34)
r
¨
=
d
r
˙
d
t
=
d
r
˙
d
r
d
r
d
t
=
d
r
˙
d
r
r
˙
{\displaystyle {\ddot {r}}={\frac {d{\dot {r}}}{dt}}={\frac {d{\dot {r}}}{dr}}{\frac {dr}{dt}}={\frac {d{\dot {r}}}{dr}}{\dot {r}}\!}
(35)
μ
d
r
˙
d
r
r
˙
=
l
2
μ
r
3
−
∂
U
∂
r
{\displaystyle \mu {\frac {d{\dot {r}}}{dr}}{\dot {r}}={\frac {l^{2}}{\mu r^{3}}}-{\frac {\partial U}{\partial r}}\!}
(36)
∫
μ
r
˙
d
r
˙
=
∫
(
l
2
μ
r
3
−
∂
U
∂
r
)
d
r
⇒
1
2
μ
r
˙
2
=
−
1
2
l
2
μ
r
2
−
U
(
r
)
+
E
{\displaystyle \int \mu {\dot {r}}d{\dot {r}}=\int \left({\frac {l^{2}}{\mu r^{3}}}-{\frac {\partial U}{\partial r}}\right){\mathit {d}}r\;\Rightarrow \;{\frac {1}{2}}\mu {\dot {r}}^{2}=-{\frac {1}{2}}{\frac {l^{2}}{\mu r^{2}}}-U(r)+E\!}
(37) unde E este constanta de integrare:
E
=
1
2
μ
r
˙
2
+
1
2
l
2
μ
r
2
+
U
(
r
)
{\displaystyle E={\frac {1}{2}}\mu {\dot {r}}^{2}+{\frac {1}{2}}{\frac {l^{2}}{\mu r^{2}}}+U(r)\!}
(38) unde:
U
e
f
(
r
)
=
1
2
l
2
μ
r
2
+
U
(
r
)
.
{\displaystyle U_{ef}(r)={\frac {1}{2}}{\frac {l^{2}}{\mu r^{2}}}+U(r).\!}
(39)
E
=
T
+
U
(
r
)
=
1
2
μ
(
r
˙
2
+
r
2
φ
˙
2
)
+
U
(
r
)
∼
r
(
t
)
{\displaystyle E=T+U(r)={\frac {1}{2}}\mu ({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2})+U(r)\sim r(t)\!}
(40)
μ
r
¨
−
l
2
μ
r
3
+
∂
U
∂
r
=
0
⇒
μ
r
¨
=
−
d
d
r
[
U
(
r
)
+
1
2
l
2
μ
r
2
]
{\displaystyle \mu {\ddot {r}}-{\frac {l^{2}}{\mu r^{3}}}+{\frac {\partial U}{\partial r}}=0\;\Rightarrow \;\mu {\ddot {r}}=-{\frac {d}{dr}}\left[U(r)+{\frac {1}{2}}{\frac {l^{2}}{\mu r^{2}}}\right]\!}
(41)
r
˙
{\displaystyle {\dot {r}}\!}
μ
r
˙
r
¨
=
−
r
˙
d
d
r
[
U
(
r
)
+
1
2
l
2
μ
r
2
]
{\displaystyle \mu {\dot {r}}{\ddot {r}}=-{\dot {r}}{\frac {d}{dr}}\left[U(r)+{\frac {1}{2}}{\frac {l^{2}}{\mu r^{2}}}\right]\!}
(42) deoarece:
μ
r
¨
r
˙
=
d
d
t
(
1
2
μ
r
˙
2
)
−
r
˙
d
d
r
=
−
d
r
d
t
d
d
r
=
−
d
d
t
{\displaystyle \mu {\ddot {r}}{\dot {r}}={\frac {d}{dt}}\left({\frac {1}{2}}\mu {\dot {r}}^{2}\right)\;\;-{\dot {r}}{\frac {d}{dr}}=-{\frac {dr}{dt}}{\frac {d}{dr}}=-{\frac {d}{dt}}\!}
(43)
⇒
d
d
t
[
1
2
μ
r
˙
2
+
U
(
r
)
+
1
2
l
2
μ
r
2
]
=
0.
{\displaystyle \Rightarrow \;\;{\frac {d}{dt}}\left[{\frac {1}{2}}\mu {\dot {r}}^{2}+U(r)+{\frac {1}{2}}{\frac {l^{2}}{\mu r^{2}}}\right]=0.\!}
(44) Astfel:
1
2
μ
r
˙
2
+
U
(
r
)
+
1
2
l
2
μ
r
2
=
c
o
n
s
t
{\displaystyle {\frac {1}{2}}\mu {\dot {r}}^{2}+U(r)+{\frac {1}{2}}{\frac {l^{2}}{\mu r^{2}}}=const\!}
(45) deoarece:
l
2
2
μ
r
2
=
μ
r
2
φ
˙
2
2
⇒
{\displaystyle {\frac {l^{2}}{2\mu r^{2}}}={\frac {\mu r^{2}{\dot {\varphi }}^{2}}{2}}\;\;\Rightarrow \!}
(46)
E
=
T
+
U
(
r
)
=
1
2
μ
(
r
˙
2
+
r
2
φ
˙
2
)
+
U
(
r
)
=
c
o
n
s
t
.
{\displaystyle E=T+U(r)={\frac {1}{2}}\mu ({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2})+U(r)=const.\!}
(47)
μ
r
¨
=
−
∂
U
e
f
(
r
)
∂
r
{\displaystyle \mu {\ddot {r}}=-{\frac {\partial U_{ef}(r)}{\partial r}}\!}
(48) (Mişcarea unei particule într-un potenţial efectiv)
E
=
1
2
μ
r
˙
2
+
U
e
f
(
r
)
{\displaystyle E={\frac {1}{2}}\mu {\dot {r}}^{2}+U_{ef}(r)\!}
(49)
⇒
r
˙
=
d
r
d
t
=
±
2
μ
(
E
−
U
e
f
(
r
)
)
⇒
t
=
±
∫
0
t
d
r
2
μ
(
E
−
U
e
f
(
r
)
)
+
c
o
n
s
t
≡
r
(
t
)
{\displaystyle \Rightarrow \;\;{\dot {r}}={\frac {dr}{dt}}=\pm {\sqrt {{\frac {2}{\mu }}(E-U_{ef}(r))}}\;\;\Rightarrow \;\;t=\pm \int _{0}^{t}{\frac {dr}{\sqrt {{\frac {2}{\mu }}(E-U_{ef}(r))}}}+const\equiv r(t)\!}
(50)
φ
˙
=
l
μ
r
2
=
d
φ
d
t
⇒
φ
(
t
)
=
∫
0
t
l
μ
[
r
(
t
)
]
2
d
t
+
φ
0
{\displaystyle {\dot {\varphi }}={\frac {l}{\mu r^{2}}}={\frac {d\varphi }{dt}}\;\;\Rightarrow \;\;\varphi (t)=\int _{0}^{t}{\frac {l}{\mu [r(t)]^{2}}}dt+\varphi _{0}\!}
(51) E şi l (mărimi care se conservă) căutăm
r
(
φ
)
:
{\displaystyle r(\varphi ):\!}
(52)
r
˙
=
d
r
d
φ
φ
˙
=
d
r
d
φ
l
μ
r
2
=
±
2
μ
(
E
−
U
e
f
)
⇒
{\displaystyle {\dot {r}}={\frac {dr}{d\varphi }}{\dot {\varphi }}={\frac {dr}{d\varphi }}{\frac {l}{\mu r^{2}}}=\pm {\sqrt {{\frac {2}{\mu }}(E-U_{ef})}}\;\;\Rightarrow \!}
(53)
⇒
φ
=
±
∫
r
0
r
l
r
2
2
μ
(
E
−
U
e
f
)
d
r
+
c
o
n
s
t
≡
φ
(
r
)
{\displaystyle \Rightarrow \;\;\varphi =\pm \int _{r_{0}}^{r}{\frac {l}{r^{2}{\sqrt {2\mu (E-U_{ef})}}}}dr+const\equiv \varphi (r)\!}
(54)
Ecuaţia traiectoriei [ ]
r
˙
{\displaystyle {\dot {r}}\!}
E
≥
U
e
f
(
r
)
{\displaystyle E\geq U_{ef}(r)\!}
valorile lui r pentru care
E
=
U
e
f
(
r
)
{\displaystyle E=U_{ef}(r)\!}
punctul în care
r
˙
=
0
{\displaystyle {\dot {r}}=0\!}
dacă
r
m
i
n
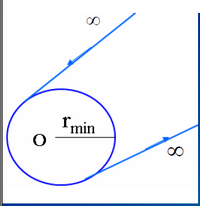
{\displaystyle r_{min}\!}
E
=
U
e
f
(
r
)
{\displaystyle E=U_{ef}(r)\!}
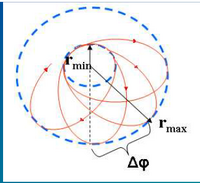
r toate rădăcinile cuprinse între
(
r
m
i
n
,
∞
)
{\displaystyle (r_{min},\infty )\!}
r
0
>
r
m
i
n
,
{\displaystyle r_{0}>r_{min},\!}
nelimitată.
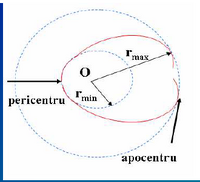
dacă ecuaţia
E
=
U
e
f
(
r
)
{\displaystyle E=U_{ef}(r)\!}
r
m
i
n
<
r
m
a
x
{\displaystyle r_{min}<r_{max}\!}
r
∈
[
r
m
i
n
,
r
m
a
x
]
{\displaystyle r\in [r_{min},r_{max}]\!}
E
≥
U
e
f
(
r
)
{\displaystyle E\geq U_{ef}(r)\!}
limitată .
întreaga traiectorie este conţinută într-o coroană circulară
Δ
φ
=
±
∫
r
m
i
n
r
m
a
x
l
r
2
2
μ
(
U
−
E
e
f
)
d
r
{\displaystyle \Delta \varphi =\pm \int _{r_{min}}^{r_{max}}{\frac {l}{r^{2}{\sqrt {2\mu (U-E_{ef})}}}}dr\!}
(55)
n
⋅
Δ
φ
=
m
⋅
2
π
;
(
n
,
m
≥
1
)
{\displaystyle n\cdot \Delta \varphi =m\cdot 2\pi ;\;(n,m\geq 1)\!}
(56)
⇒
{\displaystyle \Rightarrow \!}
Δ
φ
=
m
n
⋅
2
π
{\displaystyle \Delta \varphi ={\frac {m}{n}}\cdot 2\pi \!}
Condiţia de "închidere" a traiectoriei (raza vectoara a punctului, după ce a efectuat m rotaţii complete, îşi va regăsi valoarea iniţială)
U
(
r
)
=
{
−
k
r
k
r
2
{\displaystyle U(r)={\begin{cases}-{\frac {k}{r}}\\kr^{2}\end{cases}}\!}
(57)
Ecuaţia diferenţială a orbitei [ ] Am găsit forma generală pentru
r
=
r
(
φ
)
{\displaystyle r=r(\varphi )\!}
r
=
r
(
t
)
{\displaystyle r=r(t)\!}
E , l etc. şi căutăm
r
=
r
(
φ
)
{\displaystyle r=r(\varphi )\!}
ecuaţia orbitei .
μ
r
2
φ
˙
=
l
{\displaystyle \mu r^{2}{\dot {\varphi }}=l\!}
(58)
⇒
{\displaystyle \Rightarrow \!}
μ
r
2
d
φ
d
t
=
l
⇒
μ
r
2
d
φ
=
l
d
t
{\displaystyle \mu r^{2}{\frac {d\varphi }{dt}}=l\;\Rightarrow \;\mu r^{2}d\varphi ={\mathit {l}}dt\!}
(59)
⇒
{\displaystyle \Rightarrow \!}
d
d
t
=
l
μ
r
2
⋅
d
d
φ
{\displaystyle {\frac {d}{dt}}={\frac {l}{\mu r^{2}}}\cdot {\frac {d}{d\varphi }}\!}
(60)
⇒
{\displaystyle \Rightarrow \!}
d
2
d
t
2
=
l
μ
r
2
d
d
φ
(
l
μ
r
2
d
d
φ
)
{\displaystyle {\frac {d^{2}}{dt^{2}}}={\frac {l}{\mu r^{2}}}{\frac {d}{d\varphi }}\left({\frac {l}{\mu r^{2}}}{\frac {d}{d\varphi }}\right)\!}
(61)
μ
r
¨
−
l
2
μ
r
3
=
−
∂
U
∂
r
=
f
(
r
)
{\displaystyle \mu {\ddot {r}}-{\frac {l^{2}}{\mu r^{3}}}=-{\frac {\partial U}{\partial r}}=f(r)\!}
(62)
⇒
{\displaystyle \Rightarrow \!}
1
r
2
d
d
φ
(
l
μ
r
2
d
r
d
φ
)
−
l
2
μ
r
3
=
f
(
r
)
.
{\displaystyle {\frac {1}{r^{2}}}{\frac {d}{d\varphi }}\left({\frac {l}{\mu r^{2}}}{\frac {dr}{d\varphi }}\right)-{\frac {l^{2}}{\mu r^{3}}}=f(r).\!}
(63)
1
r
2
⋅
d
r
d
φ
=
−
d
d
φ
(
1
r
)
{\displaystyle {\frac {1}{r^{2}}}\cdot {\frac {dr}{d\varphi }}=-{\frac {d}{d\varphi }}\left({\frac {1}{r}}\right)\!}
(64)
şi introducând
u
=
1
r
{\displaystyle u={\frac {1}{r}}\!}
l
2
u
2
μ
(
d
2
u
d
φ
2
+
u
)
=
−
f
(
1
u
)
{\displaystyle {\frac {l^{2}u^{2}}{\mu }}\left({\frac {d^{2}u}{d\varphi ^{2}}}+u\right)=-f({\frac {1}{u}})\!}
(65)
d
d
u
=
d
r
d
φ
d
d
r
=
−
1
u
2
d
d
v
{\displaystyle {\frac {d}{du}}={\frac {dr}{d\varphi }}{\frac {d}{dr}}=-{\frac {1}{u^{2}}}{\frac {d}{dv}}\!}
d
2
u
d
φ
2
+
u
=
−
μ
l
2
d
d
u
D
(
1
u
)
{\displaystyle {\frac {d^{2}u}{d\varphi ^{2}}}+u=-{\frac {\mu }{l^{2}}}{\frac {d}{du}}D\left({\frac {1}{u}}\right)\!}
(66)
(65) şi (66) sunt ecuaţiile diferenţiale ale orbitei (ecuaţia Binet) dacă se cunosc f sau U .
d
φ
=
l
d
r
μ
r
2
2
μ
(
E
−
U
e
f
(
r
)
)
=
l
d
r
μ
r
2
2
μ
(
E
−
U
(
r
)
−
l
2
2
μ
r
2
)
{\displaystyle d\varphi ={\frac {l{\mathit {dr}}}{\mu r^{2}{\sqrt {{\frac {2}{\mu }}(E-U_{ef}(r))}}}}={\frac {l{\mathit {dr}}}{\mu r^{2}{\sqrt {{\frac {2}{\mu }}\left(E-U(r)-{\frac {l^{2}}{2\mu r^{2}}}\right)}}}}\!}
(67)
⇒
{\displaystyle \Rightarrow \!}
φ
=
∫
r
0
r
d
r
r
2
2
μ
E
l
2
−
2
μ
U
l
2
−
1
r
2
+
φ
0
{\displaystyle \varphi =\int _{r_{0}}^{r}{\frac {dr}{r^{2}{\sqrt {{\frac {2\mu E}{l^{2}}}-{\frac {2\mu U}{l^{2}}}-{\frac {1}{r^{2}}}}}}}+\varphi _{0}\!}
(68)
(ecuaţie ce dă
φ
{\displaystyle \varphi \!}
r şi constantele
E
,
l
,
r
0
{\displaystyle E,l,r_{0}\!}
Făcând schimbarea de variabilă
u
=
1
r
{\displaystyle u={\frac {1}{r}}\!}
⇒
{\displaystyle \Rightarrow \!}
φ
=
φ
0
−
∫
u
0
u
d
u
2
μ
E
l
2
−
2
μ
U
l
2
−
u
2
{\displaystyle \varphi =\varphi _{0}-\int _{u_{0}}^{u}{\frac {du}{\sqrt {{\frac {2\mu E}{l^{2}}}-{\frac {2\mu U}{l^{2}}}-u^{2}}}}\!}
(69)
(ecuaţia formală a orbitei)
Problema lui Kepler [ ]
f
(
r
)
=
−
k
r
2
⇒
U
(
r
)
=
−
k
r
{\displaystyle f(r)=-{\frac {k}{r^{2}}}\;\Rightarrow \;U(r)=-{\frac {k}{r}}\!}
(70)
U
e
f
=
−
k
r
+
l
2
2
m
r
2
{\displaystyle U_{ef}=-{\frac {k}{r}}+{\frac {l^{2}}{2mr^{2}}}\!}
(71)
d
2
u
d
φ
2
+
u
=
−
m
l
2
u
2
f
(
1
u
)
{\displaystyle {\frac {d^{2}u}{d\varphi ^{2}}}+u=-{\frac {m}{l^{2}u^{2}}}f\left({\frac {1}{u}}\right)\!}
(72)
d
2
u
d
φ
2
+
u
=
−
m
l
2
d
d
u
U
(
1
u
)
{\displaystyle {\frac {d^{2}u}{d\varphi ^{2}}}+u=-{\frac {m}{l^{2}}}{\frac {d}{du}}U\left({\frac {1}{u}}\right)\!}
(73)
⇒
{\displaystyle \Rightarrow \!}
d
2
u
d
φ
2
+
u
=
m
k
l
2
{\displaystyle {\frac {d^{2}u}{d\varphi ^{2}}}+u={\frac {mk}{l^{2}}}\!}
(74)
y
=
u
−
m
k
l
2
{\displaystyle y=u-{\frac {mk}{l^{2}}}\!}
⇒
{\displaystyle \Rightarrow \!}
d
y
d
φ
2
+
y
=
0
{\displaystyle {\frac {d^{y}}{d\varphi ^{2}}}+y=0\!}
(75)
⇒
{\displaystyle \Rightarrow \!}
y
=
C
cos
(
φ
−
φ
′
)
{\displaystyle y={\mathcal {C}}\cos(\varphi -\varphi ')\!}
(76) (
C
,
φ
{\displaystyle {\mathcal {C}},\varphi \!}
Notăm:
ε
=
C
l
2
m
k
{\displaystyle \varepsilon ={\mathcal {C}}{\frac {l^{2}}{mk}}\!}
(77)
⇒
{\displaystyle \Rightarrow \!}
1
r
=
m
k
l
2
[
1
+
ε
cos
(
φ
−
φ
′
)
]
{\displaystyle {\frac {1}{r}}={\frac {mk}{l^{2}}}[1+\varepsilon \cos(\varphi -\varphi ')]\!}
(78)
φ
=
φ
0
−
∫
d
u
2
m
E
l
2
−
f
r
a
c
2
m
U
l
2
−
u
2
{\displaystyle \varphi =\varphi _{0}-\int {\frac {du}{\sqrt {{\frac {2mE}{l^{2}}}-frac{2mU}{l^{2}}-u^{2}}}}\!}
(79) însă
∫
d
x
a
+
b
x
+
c
x
2
=
1
−
c
arccos
[
−
b
+
2
x
b
2
−
4
a
c
]
a
=
2
m
E
l
2
;
b
=
2
m
k
l
2
;
c
=
−
1
{\displaystyle \int {\frac {dx}{\sqrt {a+bx+cx^{2}}}}={\frac {1}{\sqrt {-c}}}\arccos \left[-{\frac {b+2x}{\sqrt {b^{2}-4ac}}}\right]\;\;a={\frac {2mE}{l^{2}}};\;\;b={\frac {2mk}{l^{2}}};\;\;c=-1\!}
(80)
∫
d
φ
=
−
∫
d
u
2
m
E
l
2
+
2
m
k
u
l
2
−
u
2
=
−
∫
d
u
2
m
E
l
2
+
m
2
k
2
l
4
−
(
m
k
l
2
−
u
2
)
2
=
{\displaystyle \int d\varphi =-\int {\frac {du}{\sqrt {{\frac {2mE}{l^{2}}}+{\frac {2mku}{l^{2}}}-u^{2}}}}=-\int {\frac {du}{\sqrt {{\frac {2mE}{l^{2}}}+{\frac {m^{2}k^{2}}{l^{4}}}-\left({\frac {mk}{l^{2}}}-u^{2}\right)^{2}}}}=\!}
(81)
=
−
1
2
m
E
l
2
+
m
2
k
2
l
4
⋅
∫
d
u
1
−
(
m
k
l
2
−
u
2
m
E
l
2
+
m
2
k
2
l
4
)
2
{\displaystyle =-{\frac {1}{\sqrt {{\frac {2mE}{l^{2}}}+{\frac {m^{2}k^{2}}{l^{4}}}}}}\cdot \int {\frac {du}{\sqrt {1-\left({\frac {{\frac {mk}{l^{2}}}-u}{\sqrt {{\frac {2mE}{l^{2}}}+{\frac {m^{2}k^{2}}{l^{4}}}}}}\right)^{2}}}}\!}
(82)
=
−
∫
sin
ω
sin
ω
d
ω
=
−
ω
⇒
cos
ω
=
cos
(
φ
−
φ
′
)
=
m
k
l
2
−
u
2
m
E
l
2
+
m
2
k
2
l
4
{\displaystyle =-\int {\frac {\sin \omega }{\sin \omega }}d\omega =-\omega \;\;\Rightarrow \;\;\cos \omega =\cos(\varphi -\varphi ')={\frac {{\frac {mk}{l^{2}}}-u}{\sqrt {{\frac {2mE}{l^{2}}}+{\frac {m^{2}k^{2}}{l^{4}}}}}}\!}
(83)
⇒
{\displaystyle \Rightarrow \!}
φ
=
φ
′
−
arccos
[
l
2
u
m
k
−
1
1
+
2
E
l
2
m
k
2
]
{\displaystyle \varphi =\varphi '-\arccos \left[{\frac {{\frac {l^{2}u}{mk}}-1}{\sqrt {1+{\frac {2El^{2}}{mk^{2}}}}}}\right]\!}
(84) deoarece
u
=
1
r
{\displaystyle u={\frac {1}{r}}\!}
⇒
{\displaystyle \Rightarrow \!}
u
=
1
r
=
m
k
l
2
[
1
+
1
+
2
E
l
2
m
k
2
cos
(
φ
−
φ
′
)
]
=
m
k
l
2
[
1
+
ε
cos
(
φ
−
φ
′
)
]
{\displaystyle u={\frac {1}{r}}={\frac {mk}{l^{2}}}\left[1+{\sqrt {1+{\frac {2El^{2}}{mk^{2}}}}}\cos(\varphi -\varphi ')\right]={\frac {mk}{l^{2}}}[1+\varepsilon \cos(\varphi -\varphi ')]\!}
(85)
ε
{\displaystyle \varepsilon\!}
ε
>
1
,
E
>
0
:
{\displaystyle \varepsilon >1,\;E>0:\!}
hiperbola
ε
=
1
,
E
=
0
:
{\displaystyle \varepsilon =1,\;E=0:\!}
parabola
ε
<
1
,
E
<
0
:
{\displaystyle \varepsilon <1,\;E<0:\!}
elipsa
ε
=
0
,
E
=
−
m
k
2
2
l
2
:
{\displaystyle \varepsilon =0,\;E=-{\frac {mk^{2}}{2l^{2}}}:\!}
cerc .
Orbite mărginite [ ]
E
=
E
2
⇒
r
m
i
n
<
r
<
r
m
a
x
{\displaystyle E=E_{2}\;\Rightarrow \;r_{min}<r<r_{max}\!}
1
r
=
m
k
l
2
(
1
±
ε
)
{\displaystyle {\frac {1}{r}}={\frac {mk}{l^{2}}}(1\pm \varepsilon )\!}
(86) Lungimea axei mari:
a
=
l
2
2
m
k
(
1
1
+
ε
+
1
1
−
ε
=
−
k
2
E
)
{\displaystyle a={\frac {l^{2}}{2mk}}\left({\frac {1}{1+\varepsilon }}+{\frac {1}{1-\varepsilon }}=-{\frac {k}{2E}}\right)\!}
(87) Lungimea axei mici:
b
=
a
1
−
ε
2
=
−
l
2
2
m
E
{\displaystyle b=a{\sqrt {1-\varepsilon ^{2}}}={\sqrt {-{\frac {l^{2}}{2mE}}}}\!}
(88) Axa orbitei:
A
=
π
a
b
=
π
−
l
2
k
2
8
m
E
3
{\displaystyle A=\pi ab=\pi {\sqrt {-{\frac {l^{2}k^{2}}{8mE^{3}}}}}\!}
(89) Viteza areolară:
d
A
d
t
=
1
2
r
2
φ
˙
2
=
1
m
{\displaystyle {\frac {dA}{dt}}={\frac {1}{2}}r^{2}{\dot {\varphi }}^{2}={\frac {1}{m}}\!}
(90) Perioada de rotaţie
T
r
o
t
=
A
(
d
A
d
t
)
=
π
−
m
k
2
2
E
3
=
2
π
m
k
a
3
2
{\displaystyle T_{rot}={\frac {A}{\left({\frac {dA}{dt}}\right)}}=\pi {\sqrt {-{\frac {mk^{2}}{2E^{3}}}}}=2\pi {\sqrt {\frac {m}{k}}}a^{\frac {3}{2}}\!}
(91) (Legea a treia a lui Kepler)
f
=
−
k
r
2
=
−
G
M
m
r
2
{\displaystyle f=-{\frac {k}{r^{2}}}=-G{\frac {Mm}{r^{2}}}\!}
(92)
T
r
o
t
=
2
π
μ
k
a
3
2
=
β
a
3
2
{\displaystyle T_{rot}=2\pi {\sqrt {\frac {\mu }{k}}}a^{\frac {3}{2}}=\beta a^{\frac {3}{2}}\!}
(93)
unde
β
=
2
π
1
G
(
M
+
m
)
{\displaystyle \beta =2\pi {\sqrt {\frac {1}{G(M+m)}}}\!}
(94) este acelaşi pentru toate planetele dacă
M
≫
m
{\displaystyle M \gg m }
Vezi şi [ ] Resurse [ ] 































































![{\displaystyle \mu {\ddot {r}}-{\frac {l^{2}}{\mu r^{3}}}+{\frac {\partial U}{\partial r}}=0\;\Rightarrow \;\mu {\ddot {r}}=-{\frac {d}{dr}}\left[U(r)+{\frac {1}{2}}{\frac {l^{2}}{\mu r^{2}}}\right]\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/ff58f83626c975498ff8656747e4c9567d62d1f0)

![{\displaystyle \mu {\dot {r}}{\ddot {r}}=-{\dot {r}}{\frac {d}{dr}}\left[U(r)+{\frac {1}{2}}{\frac {l^{2}}{\mu r^{2}}}\right]\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/403445c1ed25283827e21793c410da7f2233e0c3)

![{\displaystyle \Rightarrow \;\;{\frac {d}{dt}}\left[{\frac {1}{2}}\mu {\dot {r}}^{2}+U(r)+{\frac {1}{2}}{\frac {l^{2}}{\mu r^{2}}}\right]=0.\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/e37c8f603b87a8f5ce6353ff4b09dc1c6eaf6bcc)






![{\displaystyle {\dot {\varphi }}={\frac {l}{\mu r^{2}}}={\frac {d\varphi }{dt}}\;\;\Rightarrow \;\;\varphi (t)=\int _{0}^{t}{\frac {l}{\mu [r(t)]^{2}}}dt+\varphi _{0}\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/dedbfc5f0c742ee719dd82088fe6fc19005271e8)










![{\displaystyle r\in [r_{min},r_{max}]\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/22779a4503f27a7c33bea112019a2c696635aad3)
































![{\displaystyle {\frac {1}{r}}={\frac {mk}{l^{2}}}[1+\varepsilon \cos(\varphi -\varphi ')]\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/faf7d03dddf69b6c3618265f47e211b6e63f66a6)

![{\displaystyle \int {\frac {dx}{\sqrt {a+bx+cx^{2}}}}={\frac {1}{\sqrt {-c}}}\arccos \left[-{\frac {b+2x}{\sqrt {b^{2}-4ac}}}\right]\;\;a={\frac {2mE}{l^{2}}};\;\;b={\frac {2mk}{l^{2}}};\;\;c=-1\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/c4093aabbe2be7c7810fb81735c6a486637cc815)



![{\displaystyle \varphi =\varphi '-\arccos \left[{\frac {{\frac {l^{2}u}{mk}}-1}{\sqrt {1+{\frac {2El^{2}}{mk^{2}}}}}}\right]\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/b2b28d0bff3774295f7537bb903e8520333d4d18)
![{\displaystyle u={\frac {1}{r}}={\frac {mk}{l^{2}}}\left[1+{\sqrt {1+{\frac {2El^{2}}{mk^{2}}}}}\cos(\varphi -\varphi ')\right]={\frac {mk}{l^{2}}}[1+\varepsilon \cos(\varphi -\varphi ')]\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/8f3fb317fb3c7c4b4b35ff129dfe060ab4619a55)




























